A frequent question I receive is related to the underground systems for water storage and management we work with, that have an envelope of geotextile, is: how is it that, the geotextile does not get clogged with silts and fines? It is an interesting question and though the easiest thing to say would be to explain that the system have been successfully used since 1986, and even before, without observations.
However, saying this sometimes is not enough, in this industry one works with a lot of engineers, and myself being an engineer, we want to know why and not only that, but have proof of it.
Though one could say that the existence of ad-hoc geotextiles have existed maybe since the first textiles where developed, our earliest human ancestors, normally used textiles to clothe themselves, or to use as vessels for carrying water or other substances. It would have probably been many years before textiles would have been available in larger enough quantities to use them for other purposes other than for essential personal use.
The interesting thing though is that I came to write about this topic, because of another reason that has nothing to do with textiles or tanks, but rather a personal hobby I have. This hobby, that I very much enjoy, is home brewing my beer. I am subscribed to Hombrewer magazine and in the Autumn 2011 edition, page 22, they had an article on particle settlement, that has precisely to do with this topic. The article titled "Clarification of Beer" explains how to determine the velocity of descent of particles in suspension, their terminal velocity and finally with this and having a distance of settlement, the time for settlement. The basic components of this system then is represented by this diagram below:
Where:
Fd = Force of drag
Fb = Force of bouyancy
Fg = Force of gravity
I found this representation quite interesting and the following formula is used in the calculations.
Where: v = settling velocity (m/s)
g = acceleration due to gravity (9.8 m/s2)
ρ = density of water
ρs = density of particle
V = volume of particle
Cd = drag coefficient
A = projected area in the direction of motion (m2)
However it makes reference to a particle or solid in suspension that is not subject to the force of capillary action.
Capillary action is present in soil, as the spaces between granules act as capillary tubes. As such we can conclude that a more appropriate model for fine particles should change to consider this. Saying this, though we could make and endless regression where we could consider every particle in a soil profile to be under this influence, and it is... to an extent, however the difference in behaviour therefore lies in the particle densities and volumes that where mentioned above. This comparative differences are what would define "free" particles or that are in suspension, as particles that are freer to move in the soil media. The important aspect that we should consider is that this modelling is relevant for particles in suspension. As such, for example in the typical installation that we deal with, where sand is utilized, the sand is not in suspension, hence limiting the "endless" regression.
Taking the previous into account we can update our model and diagram to include the following, we can add another vector, Fc, Capillary Force, to the model as represented below.
Where:
Fc = Force of capillarity
However there is more to this than just including the concept of capillarity. Capillarity not only acts because of water cohesive force, that is manifested in waters surface tension, but also through water's adhesive force. We must remember that the difference between cohesion, that is the force of same molecules attracting to each other, and adhesion, the force of different molecules attracting to each other. As such, for our purposes, that particles should be uptaken against the force of gravity is also dependant that the suspended particle should not adhere to the particles not in suspension.
If we analyse these forces then, we can take the liberty and a assume a value of the force of drag as negligible and the force of buoyancy as that which allows the smaller particles to be free or in suspension, but for our effects, do not enter into our equations either.
We need to then determine the force pushing upwards, that will take the particle in suspension in the same direction:
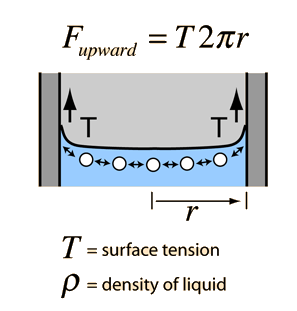 |
| source: http://hyperphysics.phy-astr.gsu.edu/hbase/surten2.html#c6 |
Effect of temperature in degC on surface tension of water in units of mJ m-2 or mN m-1(Kaye and Laby, 1973)
| Temperature | 0 | 10 | 20 | 30 | 40 |
| Surface tension | 75.7 | 74.2 | 72.75 | 71.2 | 69.6 |
The upwards force has to overcome the force of gravitation on the particle, which can be expressed in this way in terms of finding the point of equilibrium:
Fg = mg
We can then say:mg = T2πr
As we want to obtain the value of r, we arrange the variable in the following way:
r = mg/T2π
As we have the value of surface tension, we need to find the mass for a "typical" particle of silt.
Specific gravity is the ratio of the weight in air of a given volume of a material at a standard temperature to the weight in air of an equal volume of distilled water at the same stated temperature.
In natural soils, particle specific gravity will usually “range numerically from 2.60 to 2.80. Within this range, the lower values for specific gravity are typical of the coarser soils, while higher values are typical of the fine-grained soil types. Values of the specific gravity outside the range of values given may occasionally be encountered in soils derived from parent materials which contained either unusually light or unusually heavy minerals.” [Ritter and Paquette 1960, p 182]
To use a worst case scenario of sediments or fines with the highest specific gravity we can consider clay or silty clay that can have specific gravities of up to 2.9, this is also heavier than quartz that has a specific gravity of 2.65, in fact most of sand is made of quartz, and as it is the media recommend for providing the capillarity and is not in suspension, we could also presume that the particles in suspension have a lower specific gravity than quartz sand.
In this case a consider what would a silt particle similar to a small sand sand grain we can assume the following, a diameter of 0.060 mm, that implies a volume of 2.51e-10 m3, and a specific gravity of 2.65 for mineral quartz, this gives a value of 0.67 mg.
If we replace the value in the equation we obtain the following:
r = (6.7e-7 * 9.8) / (72.75e-3 * 2 * 3.14)
Which provides us with the result:
r = 14.4 μm
This can be expressed as a diameter which in the case will be 28.8 μm, which will serve a reference for pore sizes. This pore size is practically on the border of what has been defined as Mesopore and Micropores 1.
This then is the size of the capillary that provide equilibrium so that a particle smaller than the size of a grain of sand to remain in suspension. The capillary radius depends on the the particle size of the media and it has been classified in the following manner.
 |
| source:http://upload.wikimedia.org/wikipedia/commons/6/65/SoilTextureTriangle.jpg |
| Soil Texture | ||||
| Coarse | ||||
| Sand | ||||
| Fine Sand | ||||
| Loamy Sand | ||||
| Gravel/Cobble in Coarse Texture | ||||
| Moderately Coarse | ||||
| Loamy Fine Sand | ||||
| Sandy Loam | ||||
| Fine Sandy Loam | ||||
| Medium | ||||
| Gravel/Cobble in Medium Texture | ||||
| Very Fine Sandy Loam | ||||
| Loam | ||||
| Moderately Fine | ||||
| Sandy Clay Loam | ||||
| Silt Loam | ||||
| Clay Loam | ||||
| Fine | ||||
| Sandy Clay | ||||
| Silty Clay | ||||
| Clay | ||||
| Peats and Mucks | ||||
A ratio is obtained by dividing of porosity percentage with its complement, for example: in clay loam the pore space (49%) makes up almost the same amount of volume as the volume of soil particles (51%); multiply the ratio 49/51 times the 0.063 mm particle diameter to get the average pore size of 0.061 mm.
It is now interesting to see what are typical average pore sizes for soils, for example sandy loam 90μm, clay loam 61μm 2.
As the height of a capillary depends on the weight of the column of water, this is directly related to the radius of the capillary, as such the smaller the diameter of the capillary the higher the the column of water. This then produces a dichotomy in terms of that the smaller the particle size gets, eventually you get to clay sized particles that do not have much infiltration capacity and do not behave in a manner that provides capillary action.
From the above then we could conclude that the pore size we see in sandy loam, 90μm, for example is too small to provide the capillary action that we require of 28.8 μm, that we have previously determined as what would provide a capillary force that would overcome the force of gravity that the suspended particle is subject to. The situation is though that the sand, or for that case practically any soil media, is irregular and provides pore sizes that very often are much smaller that the average 90μm we calculated, as well as it providing spaces that are also larger. To illustrate this we can see the diagram below.
 |
| source: plantandsoil.unl.edu/ |
 |
| source:http://www.earthdrx.org/cap11.jpg |
In the industry we often hear of situation where supposed permeable systems become impermeable and that then need backwashing, with "sophisticated" technologies. Wouldn't it be more sophisticated to have systems that does not need maintenance or a costly backwashing system, that would not be required in the first place, if the application was designed correctly? There are many examples of these, if we were to analyse these in more details we could observe that source or cause of the clogging resides in both what we have described above, as well as other elements, that will probably include biological activity.
There are examples of these that come to mind, however to delve into them would be an odious practice.
Conclusions
Having analysed all of the above information what can be concluded is that if underground water management systems are installed correctly, with a suitable layer of soil media that provide capillarity, experience has shown that geotextiles do not clog.
This is possible due to the fact that it is possible to infer that there are spaces where capillary radii are smaller than those required to provide enough force to overcome gravity, that it in fact acts, literally, as a micro physical mechanism that provides a cleaning action that maintains the geotextile clean and free of clogging.
References:
Having analysed all of the above information what can be concluded is that if underground water management systems are installed correctly, with a suitable layer of soil media that provide capillarity, experience has shown that geotextiles do not clog.
This is possible due to the fact that it is possible to infer that there are spaces where capillary radii are smaller than those required to provide enough force to overcome gravity, that it in fact acts, literally, as a micro physical mechanism that provides a cleaning action that maintains the geotextile clean and free of clogging.
References:
http://www.newton.dep.anl.gov/askasci/env99/env201.htm
http://140.194.76.129/publications/eng-manuals/em1110-2-4000/c-7.pdf
http://gozips.uakron.edu/~mcbelch/documents/SpecificGravityofSoils.ppt
http://wwwrcamnl.wr.usgs.gov/uzf/abs_pubs/papers/nimmo.04.encyc.por.ese.pdf
T.J. Marshall, J.W. Holmes, and C.W. Rose (1996), Soil Physics, 3rd Edition, 42-45



No comments:
Post a Comment